Allocation

Allocation is the process by which experimental units are assigned to experimental groups. It can be achieved using various strategies for example a complete randomisation, a block randomisation or randomisation within matched pairs.

Content:

• Randomisation
• What is randomised?
• Randomisation strategy: complete randomisation or block randomisation?
• Spreadsheet generated by the EDA
• Other randomisation procedures
• Simple randomisation
• Computer generated
• Numbers out of a hat
• Latin squares

In the EDA diagram, a group is subjected to an allocation process, which produces several groups. The following diagram represents a pool group allocated into two groups. Further information about the randomisation strategy and procedure is contained in the properties of the allocation node.

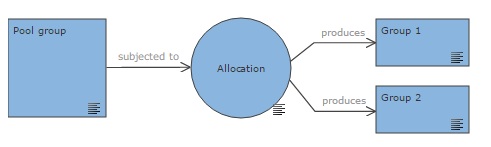
Randomisation

It is crucial that the allocation process is carried out using an appropriate strategy such as those described below as it prevents the researchers from influencing the allocation subconsciously, which is a risk if animals are assigned to groups by a process involving human judgement. However well-intentioned the experimenter is about not being biased, a ‘haphazard’ allocation is not truly random and it compromises the statistical validity of any results obtained, systematic reviews have shown that such experiments are more likely to report statistically significant results.

Randomisation is a process used to ensure that each experimental unit has an equal probability of receiving a particular treatment. Together with allocation concealment, randomisation helps minimise selection bias and reduce systematic differences in the characteristics of animals allocated to treatment groups.

Randomisation is used to allocate experimental units to treatment groups, but the principle is also relevant throughout the whole experiment. For example animal cages should be housed in a random order on the shelves and all measurements should be done in a random order (preferably with the investigator also being blinded to the treatment received by each experimental unit).

Back to top

What is randomised?

In a situation where different groups of animals receive different doses of a systemic drug treatment, animals are randomised into treatment groups. 

In contrast, in a situation where the same group of animal is used to test several doses of the drug treatment, with a wash out period between two doses, then each animal provides several experimental units, one per test period. As the experimental units (animal for one test period) are allocated into treatments, it is effectively the order of the treatments which is randomised to the animals.

Back to top

Randomisation strategy: complete randomisation or block randomisation?

Experimental units can be allocated into treatment groups using a complete randomisation or a randomisation within blocks and/or factors. A Complete randomisation assumes that all animals are simultaneously randomised to the treatments without taking any other variable into account. In other words the independent variable(s) of interest (i.e. treatment) are the only thing which might influence the outcome measure. Thus it is rarely appropriate as the result of an experiment can often be influenced by many variables. A complete randomization would only be appropriate if the expected effect size is large and/or there is relatively low variability between animals of the same treatment group. 

A randomisation within blocks is a randomisation which uses at least one of the nuisance variables as a blocking factor. It can also be called restricted or stratified randomisation. Introducing a blocking factor essentially splits up the experiment into smaller sub-experiments; randomisation is then done within each of the categories of the blocking factor (i.e. each block). Ideally, each of the treatments should be administered in a balanced way within each block. The blocking factor should also be included in the analysis to reduce the variability within the groups and increase the precision of the estimate of the effect of treatment, thus increasing the ability to detect a real effect with fewer experimental units. However, it is important to consider that blocking uses up degrees of freedom and thus reduces the power if the nuisance variable does not have a substantial impact on variability. See the nuisance variable section for more information and examples of sources of variability that can be used as a blocking factor.

If animals with different characteristics are subjected to an intervention, for example males and females, and sex is a factor of interest in the analysis, the randomisation strategy should then be a randomisation within factors so that the treatment groups can be balanced and contain the same proportion of female animals. Blocking factors and animals characteristics allocated separately can be indicated on the diagram as in the image below. In the properties of the allocation node, the randomisation strategy can be described as a complete randomisation, a randomisation within blocks, within factors, or within blocks and factors, as shown in the image below.

Back to top

Spreadsheet generated by the EDA

Once the experiment has been drawn in the editor window, the ‘randomised allocation report’ in the TOOLS menu generates an excel spreadsheet allocating experimental units into the experimental groups shown on the diagram. The randomised allocation report can also be used for blinding. It can be emailed to a colleague or collaborator who will be responsible for coding the drug syringes if the animals are subjected to a pharmacological intervention for example, or performing the surgeries if the intervention is surgical. The entire experiment can thus be carried out with the experimenter unaware of the treatment(s) the animal received. 

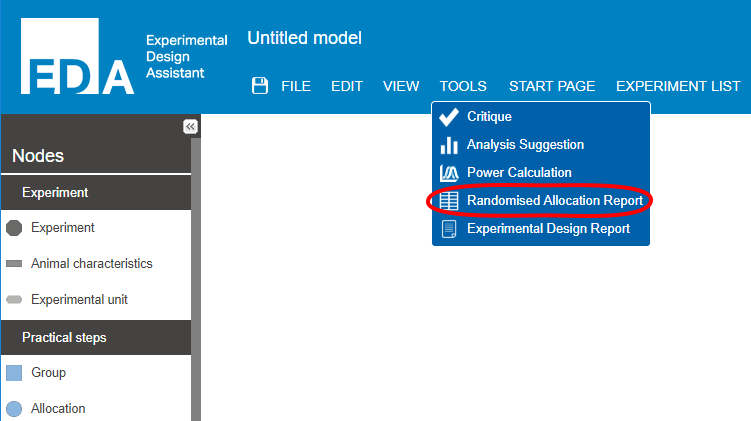
If no blocking factors or factors of interest are connected to the allocation node, the sequence will be generated based on a full randomisation. If factors are connected to the allocation node (including all variable categories, see image above), they will be accounted for in the randomisation sequence.

Please note that in the current version of the EDA, the randomisation spreadsheet randomises animals into groups, based on the number of animals indicated in the properties of the groups produced by the allocation. In experiments where the experimental unit is not the individual animal, it may not be possible to use the allocation sequence generated by the EDA. The system only supports balanced designs, with groups of equal sizes and composition. For randomisation within blocks and/or factors the system may on occasion randomise more animals than indicated in the post-allocation groups to ensure that the same number of animals are included in each stratum.

Back to top

Other randomisation procedures

Simple randomisation

For experiments with only two groups (e.g. control versus treatment), the simplest form of randomisation is to flip a coin and the side of the coin determines which group the animal is assigned to (head = control, tails = treatment). Simple randomisation can also be done by shuffling a pack of cards (red = control, black = treatment) or throwing a dice (odd = control, even = treatment). These simple methods work well for large groups but can be problematic in smaller groups where there is a greater risk of uneven numbers per group (unbalanced design) leading to reduced power; in this case the following methods can be used.

Computer generated

Consider for example an experiment with 3 treatment groups (1: control, 2: low dose and 3: high dose) with 10 animals per group. The function =Rand() in Excel can be used to generate a column of random numbers in column A. Column B would contain ten 1’s, ten 2’s and ten 3’s for each of the treatment groups and column C would contain unique identification numbers for each of the 30 animals. Sorting columns A and B by the order of column A will randomise the order of column B and each animal of column C will be allocated into treatment 1, 2 or 3 at random. 

Numbers out of a hat

Ten 1’s, ten 2’s and ten 3’s could be written on 30 pieces of paper which are folded and placed in a receptacle. After mixing, a paper is withdrawn and the first animal is assigned to the treatment number indicated, and so on.

Latin squares

Latin squares are useful to allocate experimental units to treatment groups when two blocking factors are present. Allocation using this technique is based upon the assumption that the interaction between both blocking factors is minimal and the factors are independent of each other. Technically speaking, a Latin square is not a method of randomisation in itself but experimental units can be allocated to treatment groups via randomisation of a Latin square.

In a Latin square, the two blocking factors are defined by the rows and columns, the letters inside the cells represent the treatments. Below is an example of a 3 x 3 Latin square built using the cycling method:

Note that each treatment occurs only once per row and once per column.

Other methods can be used to generate Latin squares, including the group or the product method. For more information, click here: http://www.maths.qmul.ac.uk/~rab/DOEbook/doeweb6.pdf.

Online Latin square generators can also be used, e.g.: http://hamsterandwheel.com/grids/index2d.php.

Example: crossover design

In animal studies, the largest source of variability can be the animal-to-animal variability. To account for this, a crossover design can be used where each animal is used as its own control. Latin squares are especially useful to balance the order of treatments in crossover experiments 

Consider an experiment comparing the effect of two treatments (A and B) and a control (C) where each animal receives all three treatments, separated by a one week wash out period. This is effectively a design with two blocking factors. The experimental unit is an animal for a test period and each animal provides three experimental units. Six animals are used in this experiment thus the total number of experimental units in the experiment is 18, with n=6 per treatment group. The two blocking factors are the animals (with six categories forming the columns) and the test periods (with 3 categories forming the rows).

	The order of treatments can be randomised for each animal using Latin squares. Because there are twice as many animals as there are test periods and treatments, two squares are needed (blue square and green square)
	Then the rows and columns of the Latin squares need to be randomly permuted. Thus, animal 1 will receive the control on the first week, treatment A on week 2 and treatment B on week 3, while animal 2 will receive treatment A, then the control, then treatment B, and so on.

Back to top

References and further reading

BATE, S. T. & CLARK, R. A. 2014. The Design and Statistical Analysis of Animal Experiments, Cambridge University Press.

BEBARTA, V., LUYTEN, D. & HEARD, K. 2003. Emergency medicine animal research: does use of randomization and blinding affect the results? Acad Emerg Med, 10, 684-7.

FESTING, M. F. W., OVEREND, P., GAINES DAS, R., CORTINA BORJA, M. & BERDOY, M. 2002. The design of animal experiments: reducing the use of animals in research through better experimental design, London UK, Royal Society of Medicine.

VESTERINEN, H. M., SENA, E. S., FFRENCH-CONSTANT, C., WILLIAMS, A., CHANDRAN, S. & MACLEOD, M. R. 2010. Improving the translational hit of experimental treatments in multiple sclerosis. Mult Scler, 16, 1044-55.

FESTING, M. F., http://www.3rs-reduction.co.uk/html/5__avoiding_bias.html [Accessed 15-01-2015]